O tema deste artigo é o cálculo de um dossel de policarbonato com suas próprias mãos. Temos que aprender a calcular os principais parâmetros da estrutura associados à sua resistência e dimensões. Então vamos.

O que calculamos
Temos que aprender a calcular:
- A espessura do policarbonato e o passo da caixa dependendo da carga de neve esperada por metro quadrado.
- Dimensões da tampa do arco (que em termos de geometria se resume a calcular o comprimento do arco).
Para esclarecer: estamos explorando maneiras de calcular o arco para raio e ângulo conhecidos do setor, bem como para o caso em que conhecemos apenas as distâncias entre os pontos extremos da superfície do arco.
- Seção mínima do tubo com uma carga de flexão conhecida.
Nesta ordem, seguiremos em frente.
Espessura de torneamento e revestimento
Vamos começar com o cálculo da carga de neve.
Antes de descobrirmos como calcular um dossel de policarbonato, formularemos algumas suposições nas quais o cálculo se baseia.
- Os dados fornecidos são relevantes para material de alta qualidade sem sinais de destruição por radiação ultravioleta. O policarbonato sem filtro UV torna-se quebradiço após 2-3 anos de operação na luz.

- Negligenciamos deliberadamente a limitada estabilidade de deformação da caixa, considerando-a absolutamente forte.
E agora - uma tabela que o ajudará a escolher a espessura ideal do policarbonato e o tom da caixa.
| Carga, kg/m2 | Dimensões da célula da caixa com espessura de policarbonato, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050 x 790 | 1200 x 900 | 1320 x 920 | 1250 x 950 |
| 900 x 900 | 950 x 950 | 1000x1000 | 1100 x 1100 | |
| 820x1030 | 900 x 1100 | 900 x 1150 | 950 x 1200 | |
| 160 | 880 x 660 | 1000 x 750 | 1050 x 750 | 1150 x 900 |
| 760 x 760 | 830 x 830 | 830 x 830 | 970 x 970 | |
| 700 x 860 | 750 x 900 | 750 x 950 | 850 x 1050 | |
| 200 | 800 x 600 | 850 x 650 | 950 x 700 | 1100 x 850 |
| 690 x 690 | 760 x 760 | 780 x 780 | 880x880 | |
| 620 x 780 | 650 x 850 | 700 x 850 | 750 x 950 | |
Arco
Cálculo por raio e setor
Como calcular o arco de um velame se conhecemos o raio de curvatura e o setor do arco?

A fórmula será semelhante a P=pi*r*n/180, onde:
- P é o comprimento do arco (no nosso caso, o comprimento de uma folha de policarbonato ou de um tubo de perfil, que se tornará um elemento da moldura).
- pi é o número "pi" (em cálculos que não exigem altíssima precisão, geralmente considerado igual a 3,14).
- r é o raio do arco.
- n é o ângulo do arco em graus.
Vamos, a título de exemplo, calcular com as próprias mãos o comprimento do arco da copa com raio de 2 metros e setor de 35 graus.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 metros.
No processo de trabalho, muitas vezes surge a situação oposta: é necessário ajustar o raio e o setor do arco a um comprimento fixo do arco. As razões são claras: o preço do policarbonato é alto o suficiente para minimizar a quantidade de resíduos.
Obviamente, neste caso o produto do setor pelo raio será igual a P/pi*180.
Vamos tentar encaixar o arco sob uma folha padrão de 6 metros de comprimento. 6/3,14*180=343,9 (com arredondamento). Além disso - uma simples seleção de valores com uma calculadora em mãos: por exemplo, para um setor de arco de 180 graus, você pode obter um raio igual a 343,9 / 180 \u003d 1,91 metros; com um raio de 2 metros, o setor será igual a 343,9 / 2 \u003d 171,95 graus.
Cálculo por acordes
Como fica o cálculo do desenho de uma cobertura de policarbonato com arco se tivermos apenas informações sobre a distância entre as bordas do arco e sua altura?
Neste caso, aplica-se a chamada fórmula de Huygens. Para usá-lo, vamos dividir mentalmente o acorde que conecta as extremidades do arco ao meio, após o que desenhamos uma perpendicular ao acorde no meio.
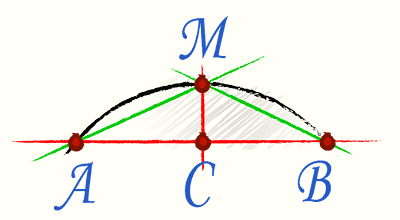
A fórmula em si tem a forma Р=2l+1/3*(2l-L), onde l é a corda AM e L é a corda AB.
Importante: o cálculo dá um resultado aproximado. O erro máximo é de 0,5%; quanto menor o setor angular do arco, menor o erro.
Vamos calcular o comprimento do arco para o caso em que AB \u003d 2 me AM - 1,2 m.
P=2*1.2+1/3*(2*1.2-2)=2.4+1/3*0.4=2.533 metros.
Cálculo da seção com uma carga de flexão conhecida
Uma situação bastante real: parte do dossel é uma viseira de comprimento conhecido. Podemos estimar aproximadamente o pico de carga de neve nele. Como escolher um tubo de perfil de tal seção para vigas para que não dobre sob carga?

Observação! Deliberadamente, não tocamos em como calcular a carga no velame. A avaliação da carga de neve e vento é um tópico completamente autossuficiente para um artigo separado.
Para calcular, precisamos de duas fórmulas:
- M = FL, onde M é o momento fletor, F é a força aplicada na extremidade da alavanca em quilogramas (no nosso caso, o peso da neve na viseira) e L é o comprimento da alavanca (o comprimento da viga que suporta a carga da neve, de ponta a ponta de fixação) em centímetros.
- M/W=R, onde W é o momento de resistência e R é a resistência do material.
E como esse monte de valores desconhecidos nos ajudará?
Por si só, nada. Alguns dados de referência estão faltando para o cálculo.
| grau de aço | Força (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Referência: Os aços St3, St4 e St5 são normalmente utilizados para tubos profissionais.
Agora, com base nos dados que temos, podemos calcular o momento de resistência à flexão do tubo de perfil. Vamos fazer isso.
Suponha que 400 quilos de neve se acumulem em um dossel de dois metros com três vigas portantes feitas de aço St3.Para simplificar os cálculos, concordaremos que toda a carga caia na borda da viseira. Obviamente, a carga em cada viga será 400/3=133,3 kg; com uma alavanca de dois metros, o momento fletor será igual a 133,3 * 200 \u003d 26660 kgf * cm.
Agora calculamos o momento de resistência W. Da equação 26660 kgf * cm / W = 2100 kgf / cm2 (resistência do aço), segue-se que o momento de resistência deve ser de pelo menos 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Como o valor do momento de resistência nos levará às dimensões do tubo? Através das tabelas de sortimento contidas em GOST 8639-82 e GOST 8645-68 regulando as dimensões de tubos quadrados e perfilados. Para cada tamanho, eles indicam o momento de resistência correspondente e para uma seção retangular - ao longo de cada um dos eixos.
Depois de verificar as tabelas, descobrimos que o tamanho mínimo de um tubo quadrado com as características exigidas é de 50x50x7,0 mm; retangular (com orientação vertical do lado maior) - 70x30x5,0 mm.

Conclusão
Esperamos não ter sobrecarregado o leitor com uma abundância de números e fórmulas secas. Como sempre, informações adicionais sobre os métodos de cálculo e design de coberturas de policarbonato podem ser encontradas no vídeo deste artigo. Boa sorte!
O artigo te ajudou?